Zobacz także:
Aby obliczyć jakie płyną prądy w obwodzie i jakie występują spadki napięcia wykorzystuje się do tego metodę klasyczną, która bazuje na dwóch prawach Kirchhoffa [1], [2]. Oczywiście jako wspomaganie należy używać prawa Ohma.
Jako przykład posłuży układ z poniższego schematu.

Przyjmiemy, że znane nam są napięcia E1 i E2, oraz rezystancje R1, R2, R3. A naszym zdaniem będzie obliczyć prądy i spadki napięcia na rezystorach.
Na początek małe wytłumaczenie dwóch pojęć:
- węzeł – to połączenie co najmniej trzech dróg dla prądu, w dalszej części oznaczane także przez literę v
- gałąź – to wszystkie elementy połączone w szereg pomiędzy dwoma węzłami, w dalszej części oznaczane przez literę b
- oczko – zamknięta część obwodu zbudowana z gałęzi połączonych węzłami, na schemacie zaznaczone są dwa oczka (zakręcone strzałki z numerami), w rzeczywistości jest jeszcze jedno oczko zawierające E1, R1, R2, oraz E2
Na przykładowym schemacie mamy jeden węzeł a, oraz trzy gałęzie. Jedna z źródłem napięcia E1 i rezystorem R1, druga ze źródłem napięcia E2 i rezystorem R2 i trzecia z rezystorem R3.
Teraz przejdziemy do matematyki, oczywiście wszystko na symbolach. Pierwszym krokiem będzie ustalenie ile równań musimy zapisać, aby móc wszystko obliczyć. Oczywiście są na to reguły. Pierwsza z nich mówi, że dla pierwszej zasady Kirchhoffa możemy zapisać v – 1 równań. Jest to ilość, która wystarcza do obliczenia i równocześnie nie będziemy mieli żadnego równania zbędnego, mówiąc ściślej wszystkie te równania będą niezależne. Także dla drugiego prawa Kirchhoffa możemy zapisać kilka równań, a ich ilość określa wzór b – v + 1.
Według naszego przykładu będzie to:
- v – 1 = 2 – 1 = 1 – równania z pierwszego prawa Kirchhoffa
- b – v + 1 = 3 – 2 + 1 = 2 – równania z drugiego prawa Kirchhoffa
To dla którego węzła i którego oczka rozpiszemy równania to zależy tylko od nas, ważne, aby zgadzała się ilość równań niezależnych. Jedno równanie zapiszemy dla węzła a:
I3 = I1 + I2
A pozostałem dwa równania napięciowe dla oczek 1 i 2:
E1 = U1 + U3
E2 = U2 + U3
co można zapisać inaczej podstawiając prawo Ohma:
E1 = R1 * I1 + R3 * I3
E2 = R2 * I2 + R3 * I3
W ten sposób uzyskujemy układ trzech równań niezależnych, który pozwala obliczyć wszystkie prądy i napięcia w obwodzie. Ważne jest aby patrzeć na kierunki strzałek, jeżeli strzałki są zgodne ze sobą (w tym samym kierunku) to dodajemy, jeżeli są przeciwne to odejmujemy. Może się okazać po wykonaniu obliczeń, że prąd wyjdzie ujemy. Nie trzeba się tym martwić, bo to oznacza, że zaznaczyliśmy na obwodzie strzałką w przeciwnym kierunku niż rzeczywiście płynie prąd. Po dokonaniu obliczeń można nanieść korektę na schemacie i wszystkie wartości prądów będą dodatnie.
Dla lepszego przedstawienia metody zaprezentuje jeszcze jeden, bardziej skomplikowany przykład.

Ten układ jest już trochę bardziej skomplikowany. Mamy tutaj 6 gałęzi, 4 węzły. Na schemacie zaznaczyłem od razu trzy oczka, które pomogą opisać układ. Tak jak w poprzednim przykładzie zaczynamy od ustalenia ile równań jest koniecznych, aby uzyskać wynik.
- v – 1 = 4 – 1 = 3 – równania z pierwszego prawa Kirchhoffa
- b – v + 1 = 6 – 4 + 1 = 3 – równania z drugiego prawa Kirchhoffa
I następnym krokiem będzie napisane równań dla węzłów:
I1 = I4 + I6 – dla węzła a
I3 = I1 + I2 – dla węzła b
I2 + I6 = I5 – dla węzła c
I na koniec trzy równania dla napięć:
E1 = R1*I1 + R4*I4 + R3*I3 – dla oczka 1
E2 = R2*I2 + R5*I5 + R3*I3 – dla oczka 2
0 = R6*I6 + R5*I5 – R4*I4 – dla oczka 3
Te sześć równań tworzą układ równań, który pozwala wyliczyć wszystkie prądy oraz napięcia w obwodzie.
Z zachowaniem reguł o ilości równań można łatwo opisać matematycznie obwód elektryczny. Metoda klasyczna jest jedną z podstawowych metod obliczeniowych stosowanych elektrotechnice i j jest bazą dla innych. Jak pewnie niektórzy zauważą równania są bardzo schematyczne i można by po małej praktyce je wymyślić z głowy nie posługując się teorią. Dlatego też powstała metoda prądów oczkowych, która sprowadza się do tego samego, ale jeszcze łatwiej jest wypisać równania.
Pominąłem w artykule rozwiązywanie tych układów równań, ponieważ zakładam, że jak ktoś zajmuje się elektroniką to potrafi sobie poradzić z takimi zagadnieniami.
Myślę, że to nie będzie koniec artykułów na temat obliczeń w elektronice, więc zachęcam zainteresowanych tematyką do śledzenia strony, a w najbliższym czasie coś się jeszcze ukażę.




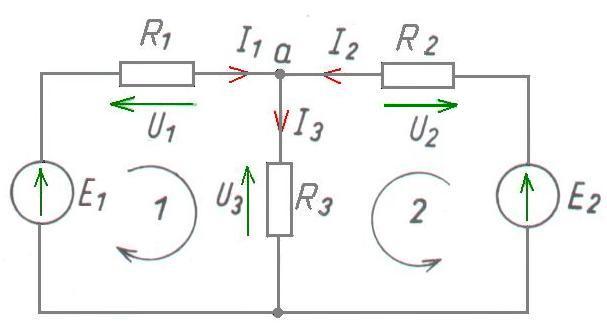
Zwroty napięć U1 i U2 powinny być narysowane w przeciwną stronę